Some geometric observations
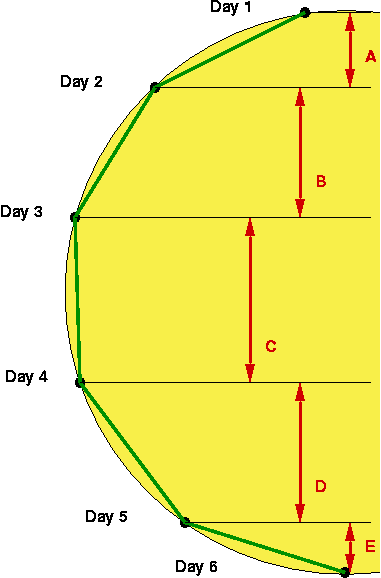 Suppose
the kids are zeroing in on a strategy which involves determining the rotational
period by dividing the distance a spot travels over some time period into
the measured circumference of the sun, and multiplying by the length
of the time period. Then in terms of the diagram to the right, they need to
measure the length of the arc connecting spot's position on Day 1 with the
position on Day 6.
Suppose
the kids are zeroing in on a strategy which involves determining the rotational
period by dividing the distance a spot travels over some time period into
the measured circumference of the sun, and multiplying by the length
of the time period. Then in terms of the diagram to the right, they need to
measure the length of the arc connecting spot's position on Day 1 with the
position on Day 6.
If we could measure the lengths of the green line segments
directly and then add them up, then you can see from the picture that we'd get
pretty close to the desired quantity. But unfortunately, from our perspective we
can only measure the lengths of the red line segments. This isn't so bad near
the center of the image, since segment C appears to be pretty close in length to
the corresponding green segment. But near the edges, it's a real problem
(segments A and E are obviously way too short). So if we add up measurements for
several consecutive days, we'll pick up some error from the days when our spot
is nearer the edge of the image.
It should be emphasized that there are pros and cons to most
decisions we make, even in scientific inquiry. If a group chooses to measure the
distances for only a couple of days near the center, then they'll have greater
multiplication of any error made in taking measurements. Thus, the particular
tactic they choose is less important than the fact that they weigh their options
from a knowledgeable standpoint.
 Suppose
the kids are zeroing in on a strategy which involves determining the rotational
period by dividing the distance a spot travels over some time period into
the measured circumference of the sun, and multiplying by the length
of the time period. Then in terms of the diagram to the right, they need to
measure the length of the arc connecting spot's position on Day 1 with the
position on Day 6.
Suppose
the kids are zeroing in on a strategy which involves determining the rotational
period by dividing the distance a spot travels over some time period into
the measured circumference of the sun, and multiplying by the length
of the time period. Then in terms of the diagram to the right, they need to
measure the length of the arc connecting spot's position on Day 1 with the
position on Day 6.